Вместо предисловия
Поскольку речь пойдет о математике, решил я тебя, дорогой читатель, сразу озадачить.
Ослик Иа загадал Винни Пуху загадку: «Мы раним, не двигаясь, мы отравляем, не прикасаясь. Мы можем принести и ложь, и правду, и нас никогда не судят по размеру. Кто мы?».
Поскольку в голове у Винни Пуха опилки, надеюсь, что среди читателей есть любители математики, и они помогут любимому сказочному персонажу решить логическую задачу. Оставим их на время в этом месте повествования, а сами отправимся дальше.
Лирикам и другим не любителям математики
Сейчас предстоит сложная задача: доказать гуманитариям, что без математики жизнь прожить можно, но сложно, что не стоит обделять себя, пытаясь отстраниться от существенной части человеческого знания. В качестве примера возьмём для определенности художников и писателей.
XIX век ознаменовался бурным развитием наук. Математика оказалась в их числе. У нас Лобачевский, на западе Риман – создали геометрию поверхности. Лобачевский и Риман явились родоначальниками неевклидовой геометрии. Наряду с этим стала развиваться теория многомерного пространства…
Достижения математики, особенно второй половины XIX и начала XX века вдохновили многих художников на поиск новых идей в искусстве. Появились такие авангардистские направления, как кубизм, сюрреализм, футуризм, абстракционизм и другие. «Ну и что?” – спросит скептически настроенный лирик. Не будем торопиться.
Лучше давайте посмотрим на картины знаменитого Сальвадора Дали. Первая так и называется: “В поисках четвертого измерения”.
На следующей картине: «Распятие, или Гиперкубическое тело» изображёно распятие Христа на объемном кресте – это видят глаза непосвящённых. А человек, знакомый с идеями многомерного пространства, знает, что это не просто крест, а развертка четырехмерного куба в трёхмерном пространстве.
Знаменитый Пабло Пикассо для создания своих полотен глубоко изучил работы французского математика Эспри Жуффре, а также работы Анри Пуанкаре. Это нашло свое отражение в его картинах. Например, в известном творении «Авиньонские девицы».
Следующая картина: «Обнажённая, спускающаяся по лестнице» – работа сюрреалиста Марсель Дюшана, хорошо знакомого с многомерной математикой и методами её визуализации.

А что же в литературе?
Литература, конечно, не осталась в стороне. Я не буду останавливаться на таком литературном жанре, как фантастика. Для него все научные открытия – основа творчества. Любители этого жанра лучше меня знают про порталы, способы перемещения во времени и другие измерения…
Хочу упомянуть две книги. Одна из них – роман Эдвина Э. Эбботта «Флатландия», написанная в 1884 году. Действие происходит в двумерном государстве – Флатландии. Автор очень интересно описывает жизнь двумерных существ, населяющих Флатландию, глазами главного героя – квадрата. По ходу повествования во сне он попадает в одномерную страну – Лайнландию, а затем, с помощью подружки сферы, узнает о существовании трехмерного пространства. После этого квадрат делает смелое предположение о существовании четырех, пяти и шестимерных пространств. Уже в XX веке эту тему развили другие писатели.
«Приключения Алисы в Стране чудес» – книга, написанная и вовсе математиком. Ее автор, Чарльз Лютвидж Доджсон, в качестве прототипа главной героини взял дочку декана колледжа – Алису. В этом учебном заведении автор читал лекции по математике. Книга была издана в1864 году под псевдонимом Льюис Кэрролл. Приключениями Алисы до сих пор зачитывается весь мир…
Вообще Чарльз Лютвидж Доджсон был очень разносторонним человеком. Помимо математики, он интересовался философией, логикой, фотографией.
Надеюсь, что даже столь короткого экскурса в мир художников и литераторов будет достаточно, чтобы молодые гуманитарии подумали о том, стоит ли сбегать с уроков математики, тем самым сильно сужая свой кругозор .

Математические школы в России не нужны?
Совсем недавно один банкир – Герман Греф, – возглавляющий Сбербанк, сделал заявление, в котором назвал школы с математическим уклоном пережитком Советского Союза.
В будущем такие профессии как математик и программист будут не так востребованы, а математические школы – пережиток прошлого, заявил Герман Греф, выступая на московском международном форуме «Открытые инновации – 2018».
Прочитав эти строки, я, вместе со многими неравнодушными к состоянию образования в нашей стране людьми, был возмущен такой постановкой вопроса. Мой зрительный вектор испытал бурю эмоций, а анальный вектор впал в праведный гнев – где справедливость. После того как эта связка векторов успокоилась, я подумал, как прав Юрий Бурлан, когда говорит на тренинге «Системно-векторная психология», что любой человек воспринимает мир и других людей только через себя.
Действительно, решил я, зачем банкиру высокообразованные вкладчики. Нормальный банкир хочет, чтобы к нему в банк приходили неучи Буратины и Коты Базилио. Вспомним диалог Лисы Алисы и Кота Базилио при дележе пяти золотых монет, которые эта парочка получила в результате ограбления глупого Буратино.
– Давай половину, – пробурчал Кот Базилио.
– Подожди Базилио. Денежки счет любят, – ответила медовым голоском Лиса Алиса.
– Сейчас в рожу вцеплюсь, – зарычал Кот Базилио. – У нас пять золотых, так? Пять на два не делятся? Не делятся! Попробуем разделить на пять. Получается один. Получай свой золотой, – отвечает Лиса Алиса, излагая свою нехитрую арифметику нежным, ласковым голоском.
– Ты меня не путай, – отвечает Кот Базилио, с трудом сдерживая раздражение.
– Базилио, ну когда я тебя путала, – говорит Лиса Алиса и продолжает,
– У нас четыре золотых, так? Четыре на пять не делятся? Не делятся! Вот я себе эту неделящуюся половину и возьму. Я же всегда рада услужить…другу.
Все, махинация Лисы Алисы завершена .

Вот вам иллюстрация мечты Г. Грефа.
Банкир счастлив, когда неграмотный человек не понимает, что за каждый взятый кредитный рубль, он принесет хозяину банка по договору два рубля в качестве процентов.
А если, не дай бог, человек получил хорошее образование, да ещё математическое. Представляете, какой ужас! Он не только внимательно прочтет кредитный договор, но и задаст кучу вопросов. С такого двести процентов прибыли не возьмёшь.
Теперь понятно, почему Г. Грефу математические школы не нужны. Ну да ладно, оставим Германа Оскаровича грустить в одиночестве, а сами отправимся дальше…
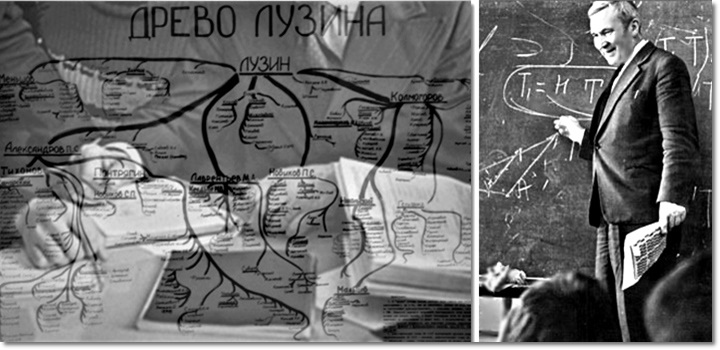
Когда я был аспирантом, довелось мне в качестве вольного слушателя учиться на механико-математическом факультете Московского университета. Однажды я увидел на стене «Древо Лузина». Захотелось подробнее узнать, кто такой Н.Н. Лузин.
Николай Николаевич Лузин родился в конце XIX века. Создатель знаменитого кружка молодых талантливых математиков, который назывался «Лузитания» (ударение на «а»). Это было сообщество развитых звуковиков. Как весело и плодотворно проводили они время. Многие «лузитаны» стали выдающимися математиками Советского Союза. Перечислю фамилии некоторых из них: П. С. Александров, А. Н. Колмогоров, Н. К. Бари, П. С. Новиков, Л. В. Келдыш и многие другие.
Например, академик А. Н. Колмогоров был прекрасным популяризатором математики. Вместе с академиком И. К. Кикоиным, он участвовал в создании математического журнала “Квант”. В 1970 году вышел первый номер этого журнала. Я хорошо помню, как мы, школьники, любившие математику, зачитывались им. С нетерпением ожидали выхода очередного номера…
Андрей Николаевич принимал непосредственное участие в реформе школьного образования в 60-е годы прошлого века. Он был автором школьных учебников по математике. Был горячим сторонником создания математических школ для одаренных детей.
Его детище – Специализированная школа-интернат № 18 физико-математического профиля при Московском государственном университете им. М. В. Ломоносова. Интернат задумывался, прежде всего, как школа научного творчества для молодежи, куда на конкурсной основе принимались школьники со всего Советского Союза.
Говоря о школе научного творчества, А. Н. Колмогоров имел в виду не только профилирующие дисциплины. Вот выдержка из его выступления на одном из заседаний педагогического совета: «Существенно, что здесь в интернате, школьники приходят в соприкосновение с творческой мыслью. Это наш запрос, но по всем предметам!… Метод работы — имитация научного исследования, шаг за шагом находить, вычислять нечто…, а не давать готовенькое…». Сейчас эта школа носит имя А. Н. Колмогорова.
Мне посчастливилось учиться в одной из московских математических школ №52. В 90-х годах, она была преобразована в гимназию №1514. Сколько выпускников этой школы поступило в ведущие вузы страны – МГУ, МИФИ, Физтех… – сейчас уже и не сосчитать. Один из моих одноклассников стал поэтом, другой академиком в компьютерной области. А учились оба в математической школе.
Физико-математические школы являются центрами сосредоточения и развития детей со звуковым вектором – детей наиболее способных к изобретениям и науке. Важно понимать, что в таких школах молодые звуковики получают возможность раскрывать свой талант не только в области математики и физики, но и максимально – в других дисциплинах, в том числе гуманитарных.

Некоторые математические школы в последние годы расширились за счет создания классов с другими направлениями: гуманитарных, медико-биологических и т.д. При этом учителя литературы, истории, параллельно работающие в различных профильных классах, отмечают, что их уроки в математических классах проходят интереснее, содержательнее, чем даже в гуманитарных. И это легко объяснимо с позиции Системно-векторной психологии: четко улавливающие смыслы, способные к глубокому сосредоточению и анализу звуковики на самом высоком уровне работают не только с цифрами, формулами и линиями, но и с текстами, информацией, фактами.
В какой бы области ни работал выпускник математической школы, он всегда проявляет себя как развитый звуковик, то есть как человек с качественным, четко настроенным мышлением. Выпускники математических школ легко и быстро осваивают новые области, достигая при этом высокого уровня компетентности. Они способны решать задачи, трудность которых заключена в сложнейшей, запутанной внутренней логике. Их вообще трудно ввести в заблуждение: у них обостренное чувство истины и лжи (когда звуковой вектор находится в связке с анальным вектором), они быстро замечают малейшие ошибки в рассуждениях – как чужих, так и своих. Они всегда до победного результата ищут точное решение.
Когда я слушал лекции Юрия Бурлана по звуковому вектору, мне было понятно, почему Юрий делал акцент на необходимости изучения математики для всех детей независимо от того, есть у ребенка интеллектуальные вектора (зрительный, звуковой) или нет. Математика как ничто другое тренирует способность к сосредоточению. Это ключевой навык для развития любого мышления, даже самого простого – наглядно-действенного. Чем активнее ребенок напрягает мозг в детстве, тем более извилистым он становится. Это правило работает для всех векторов. Ребенок любого векторального набора должен развивать свои мыслительные способности по максимуму – от этого зависит качество его будущей жизни.
Эпилог
Пришло время вспомнить о нашем сказочном герое – Винни Пухе. Тем, кто сумел помочь любимому сказочному персонажу найти правильный ответ, спасибо. Остальным сообщаю правильный ответ – «слова».
В жизни человеку каждый день приходится решать множество задач и математика, как добрая фея, всегда готова оказать помощь. Важно научиться разговаривать на её языке…
Автор Максим Авхименко
Корректор Екатерина Жаворонкова
Статья написана с использованием материалов онлайн-тренингов Юрия Бурлана “Системно-векторная психология”



